3: Resistencia al corte de los suelos
3.2: Principio de las presiones efectivas
A pesar de la verosimilitud que envuelve la ley de empujes de Coulomb, y de los muchos casos que permitieron comprobar la corrección del enunciado de la misma en el momento de ser postulada, la realidad parecía empeñarse en mostrar excepciones en las cuales la falla de una estructura de contención no podía ser explicada en razón exclusiva de la influencia de la cohesión y del rozamiento interno del material.
No obstante, en tales ocasiones debió de parecer claro que el agua intervenía en el caso. Los muros solicitados por terrenos secos o ligeramente húmedos no ofrecían problemas. Sin embargo, los suelos saturados podían provocar la ruina de las estructuras, asemejando así que el terreno perdía gran parte de su capacidad resistente a partir de una humedad determinada. De sobras es conocido que las condiciones que se dan en el trasdós de un muro de contención son proclives a favorecer la saturación de los suelos presentes, especialmente si se trata de tierras vertidas y el muro no cuenta con un drenaje adecuado.
A buen seguro durante siglos antes de los planteamientos de Coulomb, y en los decenios que los siguieron, se elucubró sobre el posible papel del agua como «lubricante» en el seno del suelo (una analogía que aún hoy día se mantiene en parte del subconsciente técnico), pero ninguna aproximación teórica demostró tal hipótesis.
No fue hasta más de 150 años después de enunciada la ley de empujes cuando Karl Terzaghi, considerado el padre de la mecánica de suelos moderna, planteó la teoría de la ley de las tensiones efectivas, resolviendo la situación.
Recordemos que los suelos constituyen un sistema trifásico formado por partículas sólidas, agua y aire, y que estas dos últimas fases se encuentran en proporción variable en los poros del material.
Supongamos un caso en el cual el suelo se encuentre saturado, y en el cual el agua que se encuentra en sus poros no drena de forma inmediata si se genera un gradiente en el seno del suelo.
En tal caso, la aplicación de una carga total (N) en el sistema, se repartirá entre la carga que soportan los contactos entre los granos (Ni), y el incremento de la presión intersticial del agua (u).
Si establecemos un plano «S» que corte por el contacto entre las dos partículas del suelo saturado (véase figura) e igualamos la fuerza total (N) que actúa sobre «S» con la presión intersticial (u) y la presión intergranular normal (Ni), podemos establecer que
N = u (S-s) + Ni
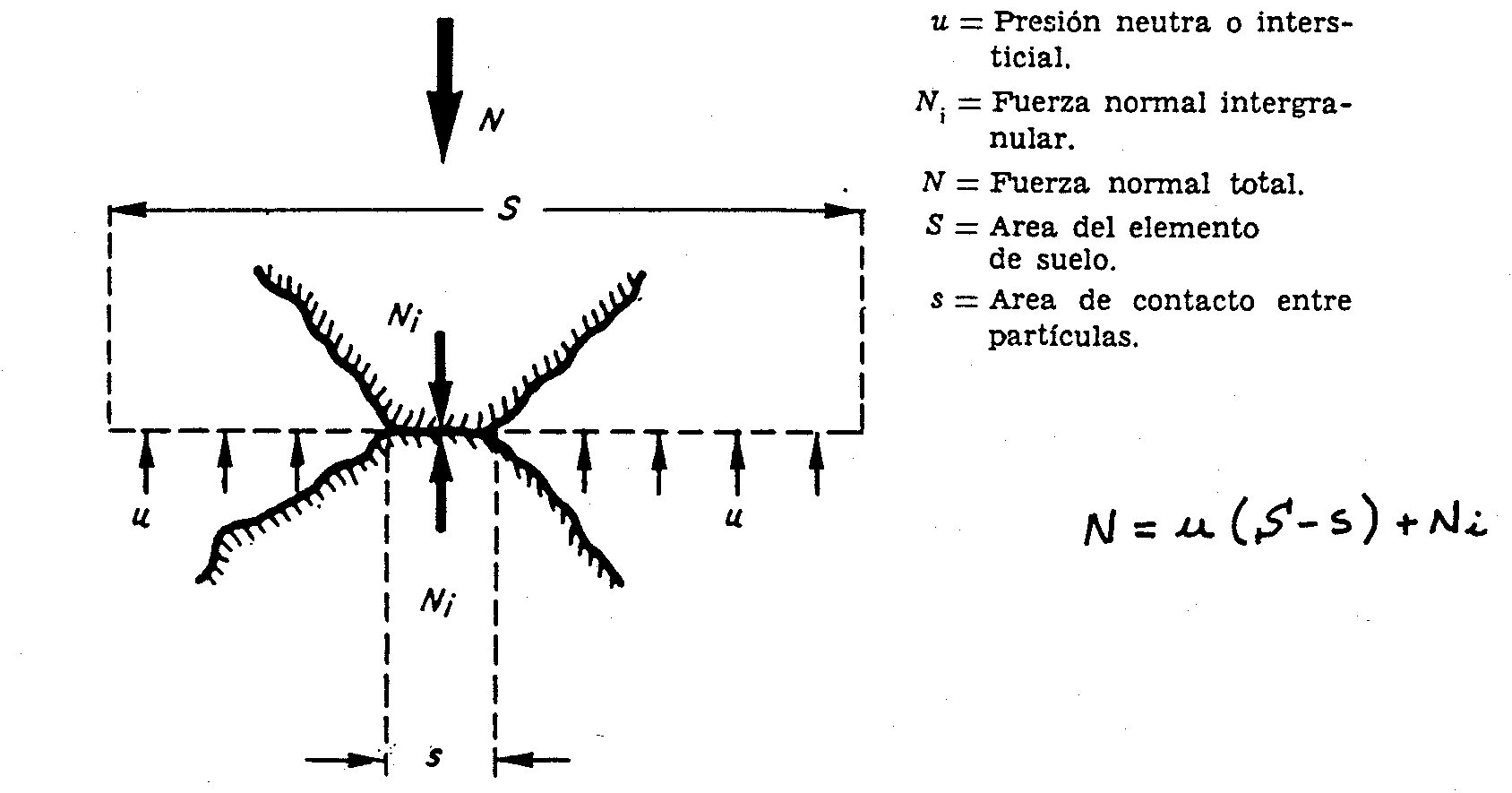
Fuente: Terzaghi & Pekc (1948): Soil mechanics in Engineering Practice.
Dividiendo las fuerzas presentes por el área S (para operar en término de presiones) y operando, se obtiene:
σ = N / S
σi = Ni / s
y por lo tanto:
σi = Ni / s la presión intergranular
σ = N / S la presión total
Con los suelos y presiones normalmente considerados en casos prácticos, la razón s/S suele ser muy pequeña, con lo cual y a efectos prácticos, la expresión se reduce a:
σi = σ – u
En tales circunstancias (si s/S = 0) Terzaghi postuló que σi es la presión de la que depende la resistencia al esfuerzo cortante de un suelo, es decir, que la presión intergranular es la «presión efectiva» (σ’). Substituyendo σi por σ’ en la expresión, obtenemos la «Ley de Terzaghi» o principio de la presión efectiva, tal vez la ley fundacional de la Mecánica del Suelo moderna:
σ’ = σ – u
En la expresión anterior σ’ representa la tensión o presión efectiva, σ la tensión o presión total y u la presión del agua o tensión intersticial. Aplicando este paradigma a la ecuación de Coulomb, consideramos:
τ = c + σ’ tg φ
Es decir, que el valor de la resistencia al corte depende, en lo que a la fuerza de rozamiento se refiere, del valor de la tensión efectiva normal al plano de corte, igual a la diferencia entre la presión normal total y la presión intersticial.
Por lo tanto, un aumento de la presión intersticial reduce la componente de fricción, que llegaría a anularse si la presión intersticial compensase el valor de la presión normal. En caso de un suelo granular (arenas) sin cohesión alguna, la resistencia del suelo resultaría nula, con efectos poco deseables.
PS. si te ha sido útil este post, no olvides visitar a alguno de nuestros anunciantes… este sitio se edita y mantiene de forma altruista, así nos puedes ayudar a costear el alojamiento.
| Situación hipotética en la que el valor de la presión intersticial iguala a la presión vertical efectiva en suelos sin cohesión
(visto en resolviendo la incógnita) |

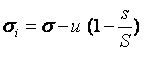









ESTA MUY INTERESANTE ESOS BLOG, PERO ME GUSTARIA QUE OPINION LE MERECE EN SUELOS EXPUESSTOS TODO EL TIEMPO EN AGUA SALADA,QUE TIPO DE MATERIAL DE RELLENO ES RECOMENDABLE PARA CONFORMAR TALUDES SUBACUATICOS
Buenas tardes Hugo,
como siempre, gracias por su interés por este humilde blog, la visión del cual, como podrá comprobar, no está enfocada al estudio especializado de la geotecnia, y menos todavía a los casos especiales; pretende (en el mejor de los casos) servir de ayuda o instrumento a los «usuarios» de la geotecnia, más que a los propios ingenieros geotécnicos, cuyos conocimientos a buen seguro superan lo que aquí se presenta.
Por tanto, en este blog no hay cabida a desarrollos tales como la geotecnia de obras portuarias, que es donde entiendo encontrará respuesta a su pregunta
Mi experiencia en obras portuarias es limitada, se lo reconozco; es un dominio por el que las circunstancias me han llevado en contadas ocasiones; en ninguna de ellas, eso sí debo decirlo, se ha planteado de forma muy específica la calidad de los rellenos vertidos en taludes subacuáticos… más bien al contrario… a los rellenos hidráulicos generalmente (cuanto menos por estos pagos) acostumbra a llegar el material menos seleccionado que puede uno imaginar, considerando en cualquier caso que las propiedades geotécnicas de tal relleno serán siempre más que deficientes. Para su contención se cuenta a posteriori con escolleras, procedimientos de mejora (por aquí generalmente jet groutings), compactaciones dinámicas (si se trata de actuar en superficie), vibrocompactación y demás.
Si le interesa el tema, le recomiendo echar un ojo a la ROM, uno de las mejores instrucciones geotécnicas que, a mi ver, ha dado este país
http://www.puertos.es/programa_rom/rom_05_94.html
saludos
joan franch
interesante, pero tengo una duda, en caso de que un suelo o roca se encuentre saturado de agua y este sometido a bajas temperaturas, transformando el agua de sus poros en hielo, la presion intertisial deberia ser mayor, pero la resistencia de la roca seria menor en relacion a la misma roca intacta o roca saturada en agua ?
el agua helada confiere al suelo o la roca una cohesión que puede ser de magnitud significativa; un ejemplo de ésto (a la inversa) son los problemas de estabilidad que se aprecian en alta montaña (Alpes, por ejemplo) debido al cambio climático; algunas vías de escalada (cara norte del Eiger, por ejemplo) son mucho más propensas (y peligrosas) ahora que cuando se escalaron por primera vez, allá por los primeros decenios del siglo pasado, debido a que los desprendimientos son mucho más frecuentes por este fenómeno.