8: Correlaciones de los parámetros del suelo a partir de los resultados de ensayos “in situ”
8.2. Correlaciones a partir del ensayo de penetración estándar SPT.
8.2.1. Introducción.
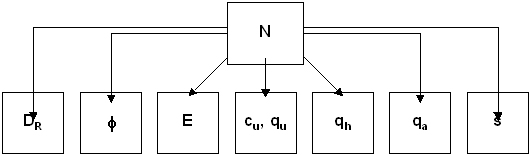
En la sección de este blog dedicada a los ensayos «in situ» se describirá con detalle la naturaleza y procedimiento de ejecución del ensayo de penetración estándar, comúnmente denominado SPT (por sus siglas inglesas «standart penetration test»). En la siguiente figura se representan de forma esquemática las relaciones que se pueden establecer entre los valores obtenidos en los ensayos de penetración estándar (SPT) y los parámetros geotécnicos característicos del terreno, entre ellos la densidad relativa Dr, ángulo de rozamiento interno, módulo de deformación…:
Donde:
Dr: densidad relativa para suelos granulares
Φ: ángulo de rozamiento interno efectivo para suelos granulares
E: módulo de deformación para suelos granulares
cu: resistencia al corte no drenada para suelos cohesivos
qu: resistencia a la compresión simple para suelos cohesivos
qh: tensión de hundimiento para cimentaciones sobre suelos granulares
qa: tensión admisible para cimentaciones sobre suelos granulares
s: asiento para cimentaciones sobre suelos granulares
Dado que el SPT es el ensayo «in situ» más utilizado y con mayor historia en la determinación de los parámetros geotécnicos, existe una cantidad ingente de relaciones empíricas entre dicho ensayo y cualquier parámetro del suelo, muchas de las cuales tienen un valor exclusivamente local. Debe realizarse siempre un examen crítico ante una correlación que parta de este ensayo y de cuya aplicación no se tenga experiencia previa, especialmente cuando se aplica a suelos coherentes.
8.2.2. Densidad relativa en suelos granulares v.s. NSPT
Terzaghi y Peck (1948) establecieron la primera de entre las más populares relaciones entre el resultado del ensayo de penetración estándar y la densidad relativa, a partir de la cual postularon lo que hoy es ya un clásico sistema de clasificación de las arenas en función de su compacidad:
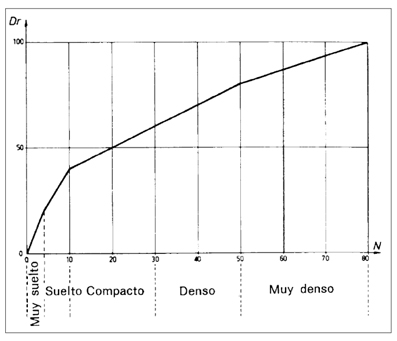 Relación entre el valor del ensayo de penetración estándar (N) y la densidad relativa, indicando la calificación del suelo en función de su compacidad (extraído de Devicenzi y Frank, 2004)
Relación entre el valor del ensayo de penetración estándar (N) y la densidad relativa, indicando la calificación del suelo en función de su compacidad (extraído de Devicenzi y Frank, 2004)
Gibbs y Holtz postularon en 1957 que el valor de NSPT no dependía solo de la densidad relativa de la arena, sino también de la presión de confinamiento. En la siguiente figura se presenta una didáctica construcción gráfica de Coffman (1960) en la que se presenta el ábaco de Gibbs y Holtz comparado con el trabajo de Terzaghi y Peck.
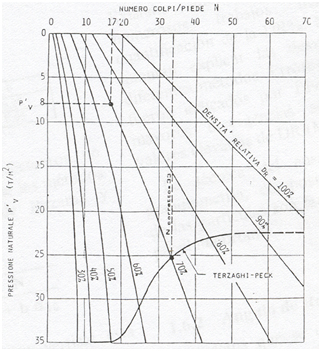 Ábaco de Gibbs y Holtz (1957), comparado con el trabajo de Terzaghi y Peck (1948). Tomado de Cestari (1990), según la elaboración de Coffman (1960).
Ábaco de Gibbs y Holtz (1957), comparado con el trabajo de Terzaghi y Peck (1948). Tomado de Cestari (1990), según la elaboración de Coffman (1960).
Para la aplicación de este ábaco debe tenerse en cuenta la compresibilidad de una arena. Un aumento en el contenido de mica o carbonato (ligado a la presencia de granos de comportamiento frágil, como bioclastos), comporta habitualmente una mayor compresibilidad de la arena. Por lo tanto, al aplicar el ábaco de Gibbs y Holtz en estos casos, debe tenerse presente que (Cestari, 1990):
– Para valores de DR < 70% los valores obtenidos del ábaco resultan superiores a los reales.
– Para valores bajos de tensión efectiva vertical (< 5 kPa), la DR (%) que se obtiene, resulta demasiado alta.
– No resulta apropiado para golpeos N < 10.
Meyerhof (1957) ajustó el anterior ábaco mediante la expresión:
DR = [ N / ( 23 σ’ + 16 ) ] 1/2
Esta expresión es válida únicamente para arenas normalmente consolidadas, presentando valores sobreestimados para arenas sobreconsolidadas.
Otro de los trabajos muy conocidos sobre este tema es el de Bazaraa (1967), cuya expresión (citada en Giuliani y Nicoll, 1982) es:
DR / 100 = 0.2236 [ N / ( a + b σ’ ) ]1/2
(la tensión vertical efectiva σ’ está expresada en T/m2)
Siendo:
|
σ’ |
a |
b |
|
<15 t/m2 |
1 |
0’2 |
|
>15 t/m2 |
3’25 |
0’05 |
Skempton (1986), resumiendo la información disponible hasta ese momento, comprueba que las correlaciones originales de Terzaghi y Peck son perfectamente válidas si se utilizan los valores normalizados N60. Según este autor esta relación puede expresarse como:
N60 / DR = a + b σ’
donde la tensión efectiva vertical está expresada en Kp/cm2. Esta expresión es análoga a las de Meyerhof y Bazaraa. Los parámetros “a” y “b” pueden ser considerados constantes en el entorno (Cestari, 1990):
85% > DR > 35%
2’5 > σ’ > 0’5 Kp/cm2
Por último, cabe comentar las expresiones propuestas en el ISOPT-1 (citadas en Ruiter, 1988):
DR = 25 N0.44 (100 σ’) -0.13
ln DR = ( 0.478 ln N ) – (0.262 ln σ’ ) -0.13 + 2.84
estando expresada la tensión efectiva en t/m2.
PS. si te ha sido útil este post, no olvides visitar a alguno de nuestros anunciantes… este sitio se edita y mantiene de forma altruista, así nos puedes ayudar a costear el alojamiento.








muy bueno
bueno
En el caso de Skempton, los valores de a y b son los mismos de Bazaraa divididos por 10?
no
Donde se pueden encontrar las referencias de los valors de a y b en este caso?
Gracias
supongo que te refieres a la referencia citada en el post Bazaraa (1967) (citada en Giuliani y Nicoll, 1982)
Pero no observo los coeficientes de regresión, correlación y/o porcentajes de asociación calculados estadísticamente, que respalden la asociación entre las variables mostradas en la gráfica y, tampoco el cálculo del tamaño de la muestra experimental que garanticen que las relaciones presentadas sean valederas desde un punto de vista de la metodología científica y de la estadística matemática .
Agustín, gracias por su participación, pero como bien podrá leer en el objeto de este blog, esto no es una publicación científica, sino una introducción dirigida a usuarios no expertos… a quienes los coeficientes de correlación… en fin
gracias
Pues buscate las publicaciones originales.
No ves que esto es más bien tipo reseña histórica de la información que hay disponible, o te cuesta mucho entender eso??? …create un blog y pones las regresiones que quieras a ver si a alguien le interesa leerlo
Saludos.
Quisiera saber si existe una correlación, ya sea, entre N60 con la cohesión, o algún otro parámetro como Peso unitario del suelo o Angulo de fricción y la cohesión. Por ejemplo de algunos autores como Perck, hanson y Tourboun.
esto es bastante controvertido, pero en caso de arcillas, y como aproximación, puede obtener la resistencia al corte sin drenaje a partir de Nspt (esto está bastante aceptado, la verdad, desde tiempos de Terzaghi), y a partir de la resistencia al corte sin drenaje, aproximar c = Su / 10 ; creo recordar que está refrendado por alguna norma del norte de Europa… pero como le digo, es algo bastante controvertido, y solo me atrevo a ponerlo en los comentarios, pero no lo postearía en el blog
🙂
en el ensayo SPT la densidad relativa de la arena puede ser determinada del material recuperado en el tubo partido por que recurrir a la formula empírica de Meyerhof o de cualquier otro
su sugerencia sería válida si tuviéramos la seguridad de que el material que entra en el tubo se encuentra inalterado y no comprimido, y que además se ha llenado el tubo con una longitud de material justamente la que se ha penetrado… lo cierto es que no es así casi nunca… o nunca… por otro lado, yendo a una correlación (por mucho que yo soy el primero que procura no abusar) se ahorra uno el trabajo de laboratorio de pesar la muestra y determinar la humedad para obtener la densidad seca… vamos, es una opinión…
ALGUNA CORRELACION PARA EL CALCULO DEL PESO UNITARIO PARA SUELOS FINOS APARTIR DEL ENSAYO DE PENETRACION ESTANDAR SPT
el SPT se correlaciona hasta con las recetas de Arguiñano, así que alguna hay, creo que de Meyerhoff y de Terzaghi… ahora no la tango a mano, pero buscando por bibliografía la encuentras